La ley de los signos

Ley de signos.

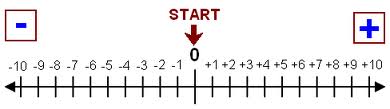
Ésta es la línea con la que todos hemos aprendido los números enteros. Si tenemos una barra marcada por barras equidistantes entre sí, marcamos la que es el cero y hacia la derecha contamos los números positivos y a la izquierda los negativos.

Ahora bien, multiplicar los signos es algo difícil de entender, para ello, comenzaremos demostrando que menos por más es menos.

Escrito de forma simbólica, si a y b son dos números enteros tenemos que demostrar que (-a)(b) =-ab

utilizando la obvia propiedad de que b-b=0 o lo que es lo mismo b+(-b)=0 utilizamos que a0= 0 o lo que es lo mismo; a(b + (-b))=0. Aplicamos la propiedad distributiva y nos queda que ab + a(-b)=0, pasamos el primer término a la derecha y tenemos que a(-b) =-ab. Un procedimiento similar se aplicará a a(-b)=-ab.

Voy a demostrar la rareza de entre las rarezas, por qué menos por menos es más. para ello, siendo x un número entero cualquiera, debemos demostrar que -(-x)=x así probaremos que que la inversa del signo negativo es positivo.

si llamamos c a -x (o sea c=(-x))   tenemos la propiedad de que x +c =0, si pasamos el término c a la derecha tenemos que x=-c, Cambiamos la variable c y nos queda que x= -(-x), que era lo que queríamos demostrar.

Si entendemos los signos como cambios de sentido, menos ir a la izquierda y más ir a la derecha (como en la barra de los números enteros) tenemos que si vamos a la derecha (+) y cambiamos de sentido(-) iremos a la izquierda, y si vamos a la izquierda(-) y cambiamos de sentido(-) iremos a la derecha