Binomio de Newton

Cuando se supone la suma de dos números enteros (o reales) cualesquiera, llamemosles a y b, cuando elevamos esta suma a cualquier potencia tenemos una regla bastante sencilla de entender, pero muy extensa cuando tenemos potencias elevadas. Nos fijaremos primero en el llamado triángulo de Tartaglia.

 Este triángulo nos indica los coeficientes que deberemos colocar en nuestro binomio desarrollado, así comenzaré con el cuadrado, debo usar el cuadrado del primero más el doble del primero por el segundo más el cuadrado del segundo, como bien se indica en la fila número 3 (empezando por arriba) del triángulo.

Así desarrollo los siguientes binomios:




¿Puedes entender la pauta de cómo se hace el resto de binomios? ¡Comenta!

Números binarios.

El código binario es el único que comprenden las máquinas

La numeración binaria quedó relegada a un sitio oscuro del cajón matemático hasta que llegó la llegada de los grandes computadores (ordenadores, como los llamamos extrañamente en España). 

El sistema binario de numeración es bastante sencillo, sólo tiene dos números 0 y 1. las sumas y las restas se realizan de la misma forma que en el sistema decimal, pero sólo podemos llevarnos una.

Voy a explicar ahora cómo se realiza el método de pasar de decimal a binario, supongamos que tenemos un número decimal, por ejemplo 143, ahora vamos a obtener su equivalente binario.

Como podéis ver lo que hago es colocar el cociente como primer número y los restos desde el último al primero

Ahora pasaré de Binario a decimal. Por ejemplo tenemos el 1110, realizamos la siguiente operación:
0x1 + 1x2 + 1x2^2 + 1x2^3 = 14

Números romanos

Los números romanos siguen una serie de reglas.

• I=1, V=5, X=10, L=50, C=100, D=500, M=1000
• A la derecha de una cifra se escribe una menor o de igual valor, y se suman los valores. Así VI es 6 y no puede existir VX.
• Si se pone un I a la izquierda de V o X le resta una unidad. Así IX es 9, si se pone un X delante de L o C se resta 10 unidades al número, se se coloca C delante de D o M se resta 100 unidades.
• Las letras se pueden repetir hasta 3 veces, sumándose su valor, las excepciones son V, L, D, que no se pueden duplicar.

En los relojes se sigue utilizando los números romanos.

Aquí tenéis una lista de números romanos.

Suma y resta de números romanos.

Utilizaré la chuleta que tan gratamente he encontrado en la wikipedia para hacer una suma mediante ese método.

36 + 25 = 61

36 = XXXVI

25 = XXV

1. No hay notación sustractiva. No hago este paso
2. Concatenamos los términos. XXXVIXXV
3. Ordenamos lo numerales de mayor a menor. XXXXXVVI
4. Simplifico los resultados reduciendo símbolos. LXI 

Ya tenemos la suma, LXI = 61

Ahora restaré 36 - 25 = 11

36=XXXVI

25=XXV

1. No hay notación sustractiva
2. Quito numerales comunes y me queda XI. Como no me quedan elementos en el segundo término hemos acabado la resta.

La resta es XI=11

No es tan complicado como dicen los puristas de los números árabes, aunque debe ser muy tedioso aplicar la multiplicación y la división con esta numeración.

Tabla de multiplicar en hoja de cálculo.

Hola, he visto práctico empezar a trastear con la hoja de cálculo de Google Docs y enseñar cómo se hace una tabla de multiplicar. He hecho la tabla hasta el 15, aunque lo que yo recomendaría es llegar hasta el 20. Es un ejercicio de memorización bastante tedioso, pero el esfuerzo compensa en la vida real.

Tabla de multiplicar de 20 x 20

 Me he guiado por el siguiente video a la hora de hacer la tabla. Es específico de Excel, pero la fórmula mágica que se pone en la casilla de 1x1 es =$A1 x B$1. Así solo corren las columnas.

A continuación os muestro el fichero que he creado. Las tabla de multiplica está en la sección de documentos, por si la queréis descargar.

Presentación de números enteros y el hotel infinito

Los números enteros surgen de la necesidad de contar en el sentido inverso, es decir, de posicionar elementos en un eje de coordenadas y de ver si una persona tiene o debe dinero.

Aquí os dejo una presentación sobre el lugar que ocupan los enteros en el mundo de los números.

Integers 101- Understanding Integers from kariknisel


Los números naturales (la mitad positiva de los números enteros) tiene un infinito que se llama numebrable. Es decir que se puede contar, para explicar este concepto contaré la historia del hotel infinito de Hilbert.

En un hotel con infinitas habitaciones ocupadas llegan un número de visitantes infinitos. ¿Se puede recolocar a todos de forma de que cada uno tenga una habitación en el hotel?


No es un problema que tenga una solución intuitiva, aunque es bastante sencilla

En un hotel infinito el número de plantas tenderá a infinito.

Lo que debemos hacer es correr a los huéspedes actuales un lugar (es decir, si el huésped está en la habitación n le reasignaremos a 2n) ahora todos los huéspedes tienen habitación par, por lo que podemos asignar a los nuevos clientes las habitaciones impares según su número m en la lista (habitación 2m-1)

Como se puede ver, cuando tratamos con infinito los problemas que tienen soluciones que con múmeros finitos no existirían. Obiviamente, si hubiera un hotel finito al completo no se pueden correr infinitas habitaciones.

El infinito es un número muy enrevesado, como la pescadilla que se muerde la cola.

La ley de los signos

Ley de signos.

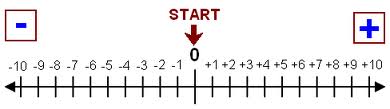
Ésta es la línea con la que todos hemos aprendido los números enteros. Si tenemos una barra marcada por barras equidistantes entre sí, marcamos la que es el cero y hacia la derecha contamos los números positivos y a la izquierda los negativos.

Ahora bien, multiplicar los signos es algo difícil de entender, para ello, comenzaremos demostrando que menos por más es menos.

Escrito de forma simbólica, si a y b son dos números enteros tenemos que demostrar que (-a)(b) =-ab

utilizando la obvia propiedad de que b-b=0 o lo que es lo mismo b+(-b)=0 utilizamos que a0= 0 o lo que es lo mismo; a(b + (-b))=0. Aplicamos la propiedad distributiva y nos queda que ab + a(-b)=0, pasamos el primer término a la derecha y tenemos que a(-b) =-ab. Un procedimiento similar se aplicará a a(-b)=-ab.

Voy a demostrar la rareza de entre las rarezas, por qué menos por menos es más. para ello, siendo x un número entero cualquiera, debemos demostrar que -(-x)=x así probaremos que que la inversa del signo negativo es positivo.

si llamamos c a -x (o sea c=(-x))   tenemos la propiedad de que x +c =0, si pasamos el término c a la derecha tenemos que x=-c, Cambiamos la variable c y nos queda que x= -(-x), que era lo que queríamos demostrar.

Si entendemos los signos como cambios de sentido, menos ir a la izquierda y más ir a la derecha (como en la barra de los números enteros) tenemos que si vamos a la derecha (+) y cambiamos de sentido(-) iremos a la izquierda, y si vamos a la izquierda(-) y cambiamos de sentido(-) iremos a la derecha

Presentación

Este blog ha sido diseñado para la asignatura de TICS del Máster del Profesorado de la UMH. Me centraré en el uso de técnicas para que los alumnos aprendan los conceptos básicos de los números enteros.